Для решения пределов существуют различные методы решений и формулы. Но самым быстрым и легким способом, а также универсальным является метод Лопиталя. Для того, чтобы успешно пользоваться этим замечательным простым способом вычисления пределов достаточно хорошо уметь находить производные различных функций. Начнём с теории.

Сформулируем правило Лопиталя. Если:

• $ \lim \limits_{x \to a} f(x) = \lim \limits_{x \to a} g(x) = 0 \text{ или } \infty $
• Существуют $ f"(a) \text{ и } g"(a) $
• $ g"(x)\neq0 $
• Существует $ \lim \limits_{x \to a} \frac{f(x)}{g(x)} $

тогда существует $ \lim \limits_{x \to a} \frac{f(x)}{g(x)} = \lim \limits_{x \to a} \frac{f"(x)}{g"(x)} $

1. Подставляем точку $ x $ в предел
2. Если получается $ \frac{0}{0} \text{ или } \frac{\infty}{\infty} $, тогда находим производную числителя и знаменателя
3. Подставляем точку $ x $ в получившийся предел и вычисляем его. Если получается неопределенность, то повторяем пункты 2 и 3

Примеры решения

Пример 1

Решить предел по правилу Лопиталя: $ \lim\limits_{x \to -1} \frac{x^2-1}{x^3+x+2} $

Решение

$$ \lim \limits_{x \to -1} \frac{x^2-1}{x^3+x+2} = \frac{0}{0} = $$ Видим, что получилась неопределенность $ \frac{0}{0} $, если подставить вместо иксов точку $ x = -1 $, а это первый сигнал о том, что необходимо применить формулу для вычисления предела. Используем её: $$ = \lim \limits_{x \to -1} \frac{(x^2-1)"}{(x^3+x+2)"} = $$ $$ =\lim \limits_{x \to -1} \frac{2x}{3x^2+1} = $$ Снова попробуем вычислить предел подставив $ x=-1 $ в последний предел, получаем: $$ =\frac{2 \cdot (-1)}{3 \cdot (-1)^2+1} = \frac{-2}{4} = -\frac{1}{2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ \lim\limits_{x \to -1} \frac{x^2-1}{x^3+x+2} = -\frac{1}{2} $$

Пример 4

Вычислить предел используя правило Лопиталя: $ \lim \limits_{x\to 0} \frac{\sin 2x-e^{5x}+1}{x-\cos x+1} $

Решение

$$ \lim \limits_{x\to 0} \frac{\sin 2x-e^{5x}+1}{x-\cos x+1} = \frac{0}{0}= $$ $$ =\lim \limits_{x\to 0} \frac{(\sin 2x-e^{5x}+1)"}{(x-\cos x+1)"} = $$ $$ =\lim \limits_{x\to 0} \frac{(\sin 2x)"-(e^{5x})"+(1)"}{(x)"-(\cos x)"+(1)"}= $$ $$ =\lim \limits_{x\to 0} \frac{2\cos 2x-5e^{5x}}{1+\sin x} =\frac{2\cos0-5e^0}{1+\sin 0}= $$ $$ =\frac{2\cdot 1-5\cdot 1}{1+0} = \frac{-3}{1} = -3 $$

Ответ

$$ \lim \limits_{x\to 0} \frac{\sin 2x-e^{5x}+1}{x-\cos x+1} = -3 $$

Подведем итог: Правило Лопиталя - это способ и метод благодаря которому можно раскрывать неопределенности вида $ \frac{0}{0} $ и $ \frac{\infty}{\infty} $ при вычислении пределов. Суть его состоит в том, что предел отношения функций равен пределу отношений производных от этих функций.

Правило говорит, что если функции f (x ) и g (x ) обладают следующим набором условий:

тогда существует . При этом теорема верна и для других баз (для указанной будет приведено доказательство).

История

Способ раскрытия такого рода неопределённостей был опубликован Лопиталем в его сочинении «Анализ бесконечно малых», изданном в году. В предисловии к этому сочинению Лопиталь указывает, что без всякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того, чтобы они предъявили свои авторские права на все, что им угодно». Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу под примечательным названием «Усовершенствование моего опубликованного в „Анализе бесконечно малых“ метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», .

Доказательство

Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида ).

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a , мы можем непрерывным образом их доопределить в этой точке: пусть f (a ) = g (a ) = 0 . Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку теорему Коши . По этой теореме получим:

,

но f (a ) = g (a ) = 0 , поэтому .

Style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/56/85e2b8bb13d6fb1ddcf88e22a4bb6ef2.png" border="0"> для конечного предела и style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/101/e8b2f2b8861947c8728d4d1be40366d4.png" border="0"> для бесконечного,

что является определением предела отношения функций.

Отношение бесконечно больших

Докажем теорему для неопределённостей вида .

Пусть, для начала, предел отношения производных конечен и равен A . Тогда, при стремлении x к a справа, это отношение можно записать как A + α , где α - (1). Запишем это условие:

.

Зафиксируем t из отрезка и применим теорему Коши ко всем x из отрезка :

, что можно привести к следующему виду: .

Для x , достаточно близких к a , выражение имеет смысл; предел первого множителя правой части равен единице (так как f (t ) и g (t ) - константы , а f (x ) и g (x ) стремятся к бесконечности). Значит, этот множитель равен 1 + β , где β - бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение , что и в определении для α :

.

Получили, что отношение функций представимо в виде (1 + β)(A + α) , и . По любому данному можно найти такое , чтобы модуль разности отношения функций и A был меньше , значит, предел отношения функций действительно равен A .

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

(x)}{g"(x)}>2M)" style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/101/e46c5113c49712376d1c357b5b202a65.png" border="0">.

В определении β будем брать ; первый множитель правой части будет больше 1/2 при x , достаточно близких к a , а тогда style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/50/2f7ced4a9b4b06f7b9085e982250dbcf.png" border="0">.

Для других баз доказательства аналогичны приведённым.

Примеры

(Только если числитель и знаменатель ОБА стремятся или к 0 ; или к ; или к .)

Wikimedia Foundation . 2010 .

Смотреть что такое "Лопиталя правило" в других словарях:

Исторически неправильное наименование одного из основных правил раскрытия неопределённостей. Л. п. было найдено И. Бернулли и сообщено им Г. Лопиталю (См. Лопиталь), опубликовавшему это правило в 1696. См. Неопределённые выражения … Большая советская энциклопедия

Раскрытие неопределенностей вида сведением предела отношения функций к пределу отношения производных рассматриваемых функций. Так, для случая, когда действительные функции f и gопределены в проколотой правосторонней окрестности точки ачисловой… … Математическая энциклопедия

Правило Бернулли Лопиталя метод нахождения пределов функций, раскрывающий неопределённости вида и. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.… … Википедия

В математическом анализе правилом Лопиталя называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу… … Википедия

В математическом анализе правилом Лопиталя называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу… … Википедия

В математическом анализе правилом Лопиталя называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу… … Википедия

Раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия, В. В. Ивлев. В пособии излагается теория дифференциального и интегрального исчис­ления функций многих переменных с примерами, задачами и упражнениями с ответами. Помимо традиционных вопросов анализа…

Инструкция

Непосредственное вычисление пределов связано, в первую очередь, с пределами рациональных Qm(x)/Rn(x), где Q и R многочлены. Если вычисляется предел при х →a (a – число), то может возникнуть неопределенность, например . Для ее устранения поделите числитель и знаменатель на (х-а). Операцию повторяйте до тех пор, пока неопределенность не пропадет. Деление многочленов осуществляется практически так же, как и деление чисел. Оно основано на том, что деление и умножение – обратные операции. Пример приведен на рис. 1.

Применение первого замечательного предела. Формула для первого замечательного предела приведена на рис. 2а. Для его применения приведите выражение вашего примера к соответствующему виду. Это всегда можно сделать чисто алгебраически или заменой переменной. Главное - не забывайте, что если синус от kx, то и знаменатель тоже kx. Пример рассмотрен на рис. 2e.Кроме того, если учесть, что tgx=sinx/cosx, cos0=1, то, как следствие, появляется (см. рис. 2b). arcsin(sinx)=x и arctg(tgx)=x. Поэтому имеются еще два следствия (рис 2с. и 2d). Возник еще достаточно широкий набор способов .

Применение второго замечательно предела (см. рис. 3а)Пределы такого типа используются для устранения неопределенностей типа . Для решения соответствующих задач просто преобразуйте условие до структуры, соответствующей виду предела. Помните, что при возведении в степень выражения, уже находящегося в какой-либо степени, их показатели перемножаются. Соответствующий пример приведен на рис. 2е.Примените подстановку α=1/х и получите следствие из второго замечательного предела (рис. 2b). Прологарифмировав по основанию а обе части этого следствия, придете ко второму следствию, в том числе и при а=е (см. рис. 2с). Сделаете замену а^x-1=y. Тогда x=log(a)(1+y). При стремлении х к нулю, у также стремится к нулю. Поэтому возникает и третье следствие (см. рис. 2d).

Применение эквивалентных бесконечно малых.Бесконечно малые функции эквивалентны при х →а, если предел их отношения α(х)/γ(х) равен единице. При вычислении пределов с помощью таких бесконечно малых просто запишите γ(x)=α(x)+o(α(x)). o(α(x)) – это бесконечно малая более высокого порядка малости, чем α(x). Для нее lim(x→a)o(α(x))/α(x)=0. Для выяснения эквивалентности используйте те же замечательные пределы. Метод позволяет существенно упростить процесс нахождения пределов, сделав его более прозрачным.

Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):

Как показывает формула выше, при вычислении предела отношений двух бесконечно малых или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Перейдём к более точным формулировкам правил Лопиталя.

Правило Лопиталя для случая предела двух бесконечно малых величин . Пусть функции f (x ) и g (x a . А в самой точке a a производная функции g (x ) не равна нулю (g "(x a равны между собой и равны нулю:

.

Правило Лопиталя для случая предела двух бесконечно больших величин . Пусть функции f (x ) и g (x ) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a . А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g (x ) не равна нулю (g "(x )≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:

.

Тогда предел отношения этих функций равен пределу отношения их производных:

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому числу, или бесконечный, то есть равный бесконечности).

Замечания .

1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .

2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов "ноль делить на ноль" и "бесконечность делить на бесконечность"

Пример 1.

x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе - производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.

Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

Применить правило Лопиталя самостоятельно, а затем посмотреть решение

Раскрытие неопределённостей вида "ноль умножить на бесконечность"

Пример 12. Вычислить

.

Решение. Получаем

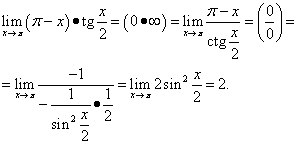
В этом примере использовано тригонометрическое тождество .

Раскрытие неопределённостей видов "ноль в степени ноль", "бесконечность в степени ноль" и "один в степени бесконечность"

Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .

Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.

Пример 13.

Решение. Получаем

.

.

Пример 14. Вычислить, пользуясь правилом Лопиталя

Решение. Получаем

Вычисляем предел выражения в показателе степени

.

.

Пример 15. Вычислить, пользуясь правилом Лопиталя

Теорема Лопита́ля (также правило Бернулли - Лопиталя ) - метод нахождения пределов функций,раскрывающий неопределённости вида и. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Точная формулировка .

Правило говорит, что если функции f (x ) и g (x ) обладают следующим набором условий:

тогда существует . При этом теорема верна и для других баз (для указанной будет приведено доказательство).

История.

Способ раскрытия такого рода неопределённостей был опубликован Лопиталем в его сочинении «Анализбесконечно малых», изданном в 1696 году. В предисловии к этому сочинению Лопиталь указывает, что безвсякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того,чтобы они предъявили свои авторские права на все, что им угодно». Иоганн Бернулли предъявил претензиина все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу подпримечательным названием «Усовершенствование моего опубликованного в „Анализе бесконечно малых“метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», 1704 .

Доказательство.

Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида ).

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a , мы можемнепрерывным образом их доопределить в этой точке: пусть f (a ) = g (a ) = 0. Возьмём некоторый x израссматриваемой полуокрестности и применим к отрезку теорему Коши . По этой теореме получим:

,

но f (a ) = g (a ) = 0, поэтому .

Для конечного предела и

Для бесконечного,

что является определением предела отношения функций.

Отношение бесконечно больших

Докажем теорему для неопределённостей вида .

Пусть, для начала, предел отношения производных конечен и равен A . Тогда, при стремлении x к a справа,это отношение можно записать как A + α, где α - O (1). Запишем это условие:

Зафиксируем t из отрезка и применим теорему Коши ко всем x из отрезка :

Что можно привести к следующему виду:

.

Для x , достаточно близких к a , выражение имеет смысл; предел первого множителя правой части равенединице (так как f (t ) и g (t ) - константы , а f (x ) и g (x ) стремятся к бесконечности). Значит, этот множительравен 1 + β, где β - бесконечно малая функция при стремлении x к a справа. Выпишем определение этогофакта, используя то же значение , что и в определении для α:

Получили, что отношение функций представимо в виде (1 + β)(A + α), и .По любому данному можно найти такое , чтобы модуль разности отношения функций и A был меньше ,значит, предел отношения функций действительно равен A .

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

В определении β будем брать ; первый множитель правой части будет больше 1/2 при x ,достаточно близких к a , а тогда .

Для других баз доказательства аналогичны приведённым.

Примеры.

(Только если числитель и знаменатель ОБА стремятся или к 0; или к ; или к .)